In an algebraic expression, if the powers of the variables are whole numbers then the algebraic expression is a polynomial.

(i) Not a polynomial.

y + \(\frac{1}{y}\) = y + y⁻¹. Here, one of the powers of y is −1, which is not a whole number. So, y + \(\frac{1}{y}\) is not a polynomial.

(ii) Not a polynomial.

5\(\sqrt{x}\) = 5x^1/2. Here, the power of x is \(\frac{1}{2}\) The power is not whole number.

(iii) Is a polynomial.

x² + 7x + 9.  Here, the powers of the variable x are 2, 1 and 0, which are whole numbers.

(iv) Not a polynomial.

2m⁻² + 7m − 5. Here, one of the powers of m is −2, which is not a whole number

(v) Is a polynomial.

10 = 10x⁰. Here, the power of x is 0, which is a whole numbers. So, 10 is a polynomial (or constant polynomial).

The coefficients of m3 in the given polynomials are as follows :

(i) 1 (ii) −\(\sqrt{3}\)  (iii) \(−\frac{2}{3}\).

A polynomial having only one term is called a monomial. Also, the highest power of the variable in a polynomial is called the degree of the polynomial.

(i) 4x⁷ is a monomial in x with degree 7.

(ii) 12x³⁵ − x⁷ is a Binomial in x with degree 35.

(ii) 3x⁸ − 2x⁵ + 8 is a Trinomial in x with degree 8.

The highest power of the variable in a polynomial of one variable is called the degree of the polynomial. Also, the highest sum of the powers of the variables in each term of the polynomial in more than one variable is the degree of the polynomial.

∴ the degree of the given polynomials is

(i) 0        …(∵ \(\sqrt{5}\) is a constant term);

(ii) 0

(iii) 2

(iv) 10

(v) 1       …(∵ p means p¹);

(vi) 5

(vii) 3     ….(∵ xyz : 1 + 1 + 1 = 3)

(viii) 10   ….(∵ m³n⁷ : 3 + 7 = 10).

The degree of the polynomial 2x² + 3x + 1 is 2.

∴ the polynomial 2x² + 3x + 1 is a quadratic polynomial.

The degree of the polynomial 5p is 1.

∴ the polynomial 5p is a linear polynomial.

The degree of the polynomial \(\sqrt{2}\)y – \(\frac{1}{2}\) is 1.

So, the polynomial \(\sqrt{2}\)y – \(\frac{1}{2}\)  is a linear polynomial.

The degree of the polynomial m³ + 7m² + \(\frac{5}{2}\)m − 7 is 3.

So, the polynomial m³ + 7m² + \(\frac{5}{2}\)m − 7 is a cubic polynomial.

The degree of the polynomial a² is 2.

∴ the polynomial a² is a quadratic polynomial.

The degree of the polynomial 3r³ is 3.

∴ the polynomial 3r³ is a cubic polynomial.

A polynomial written in either descending or ascending powers of its variable is called the standard form of the polynomial.

The given polynomial is m³ + 3 + 5m.

The standard form of the polynomial is m³ + 5m + 3.

The standard form of the polynomial is y⁵+ 2y⁴+ 3y³− y²− 7y – \(\frac{1}{2}\)

x³ – 2 = x³ + 0x² + 0x − 2

The coefficient form of the polynomial is (1, 0, 0, −2).

5y = 5y + 0

The coefficient form of the polynomial is (5, 0).

2m⁴ − 3m² + 7 = = 2m⁴ + 0m³ − 3m² + 0m + 7

The coefficient form of the polynomial is (2, 0,−3, 0,7).

The coefficient form of the polynomial \(-\frac{2}{3}\) is \((-\frac{2}{3})\) 

(1, 2, 3) Here, the number of coefficients = 3.

∴ the degree of the polynomial is 3 − 1 = 2.

∴ The standard form is x² + 2x + 3.

(5, 0, 0, 0, − 1) Here, the number of coefficients = 5.

∴ the degree of the polynomial is 5 − 1 = 4.

∴ The standard form is 5x⁴ − 1.

(− 2, 2, − 2, 2) Here, the number of coefficients = 4.

∴ the degree of the polynomial is 4 − 1 = 3.

∴ The standard form is − 2x³ + 2x² − 2x + 2.

Quadratic polynomial : 3x² + 5x; x²; 2x² + 5x + 10

Cubic polynomial : x³ + x² +x +5; x³ + 9

Linear polynomial : x + 7

Binomial : x + 7; 3x² + 5x; x³ + 9

Trinomial : 2x² + 5x + 10

Monomial : x²

The number of trees at present = a.

The number of trees increases by b in a year.

∴ the number of trees will increase by bx in x years

∴ the number of trees in the village Lat after x years will be a + bx.

Answer is : There will be a + bx trees in the village Lat.

The number of rows for parade = x

The number of students in each row = y.

∴ the total number of students for parade = x × y = xy

Answer is : The number of students present for the parade is xy.

The place value of the digit m at tens place = m × 10 = 10m

The place value of the digit n at the units place = n × 1 = n.

∴ the number formed is 10m + n.

Answer is : The required number is 10m + n.

(x³ − 2x² − 9) + (5x³ + 2x + 9)

= x³ − 2x² − 9 + 5x³ + 2x + 9      ... (Removing brackets)

= x³ + 5x³ − 2x² + 2x – 9 + 9     ... (Collecting like terms)

= 6x³ − 2x² + 2x.       ... (Adding like terms)

Answer is : 6x³ − 2x² + 2x

(− 7m⁴ + 5m³ + \(\sqrt{2}\)) + (5m⁴ − 3m³ + 2m² + 3m – 6)

= − 7m⁴ + 5m³ + \(\sqrt{2}\) + 5m⁴ − 3m³ + 2m² + 3m – 6 

= − 7m⁴ + 5m⁴ + 5m³  − 3m³ + 2m² + 3m + \(\sqrt{2}\) – 6  ... (Collecting like terms)

= − 2m⁴ + 2m³ + 2m² + 3m + \(\sqrt{2}\) – 6 

Answer is : − 2m⁴ + 2m³ + 2m² + 3m + \(\sqrt{2}\)  – 6 

(2y² + 7y + 5) + (3y + 9) + (3y² − 4y – 3)

= 2y² + 7y + 5 + 3y + 9 + 3y² − 4y – 3

= 2y² + 3y² + 7y + 3y − 4y + 5 + 9 − 3

= 5y² + 6y + 11

Answer is : 5y² + 6y + 11

(x² − 9x + \(\sqrt{3}\)) – (− 19x + \(\sqrt{3}\) + 7x²)

= x² − 9x + \(\sqrt{3}\) + 19x − \(\sqrt{3}\) − 7x²

= x² − 7x² − 9x + 19x + \(\sqrt{3}\) − \(\sqrt{3}\)

= − 6x² + 10x

Answer is : − 6x² + 10x

(2ab² + 3a²b − 4ab) − (3ab − 8ab² + 2a²b)

= 2ab² + 3a²b − 4ab − 3ab + 8ab² − 2a²b

= 2ab² + 8ab² + 3a²b − 2a²b − 4ab − 3ab

= 10ab² + a²b − 7ab

Answer is : 10ab² + a²b − 7ab

(2x) × (x² − 2x −1)

= 2x³ – 4x² – 2x

Answer is : 2x³ – 4x² – 2x

(x⁵ – 1) × (x³ + 2x² + 2)

= x⁵(x³ + 2x² + 2) −1(x³ + 2x² + 2)

= x⁸ + 2x⁷ + 2x⁵ − x³ − 2x² − 2

Answer is : x⁸ + 2x⁷ + 2x⁵ − x³ − 2x² − 2

(2y + 1) × (y² − 2y³ + 3y)

= 2y(y² − 2y³ + 3y) + 1(y² − 2y³ + 3y)

= 2y³ – 4y⁴ + 6y² + y² − 2y³ + 3y

= 2y³ − 2y³ – 4y⁴ + 6y² + y² + 3y

= – 4y⁴ + 7y² + 3y

Answer is : – 4y⁴ + 7y² + 3y

x³ – 64 = x³ + 0x² + 0x – 64    ... (Index form of the polynomial)

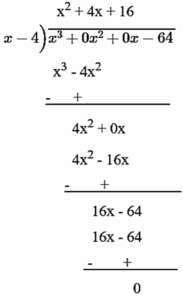
Dividend = Divisor × Quotient + Remainder

x³ – 64 = (x − 4) × (x² + 4x + 16) + 0

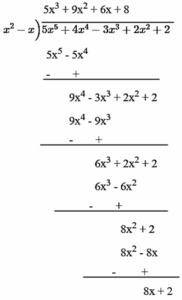
Dividend = Divisor × Quotient + Remainder

5x⁵ + 4x⁴ − 3x³ + 2x² + 2 = (x² – x) × (5x³ + 9x² + 6x + 8) + 8x + 2

Length of the rectangular farm = (2a² + 3b²) m

Breadth of the rectangular farm = (a² + b²) m

The total area of the farm = Length of the rectangular farm x Breadth of the rectangular farm

= (2a² + 3b²) × (a² + b²)

= 2a² (a² + b²) + 3b² (a² + b²)

= 2a⁴ + 2a²b² + 3a²b² + 3b⁴

= (2a⁴ + 5a²b² + 3b²) sq. meter

Side of the square plot = (a² − b²) meter.

Area of the square plot = (side) ²

= (a² − b²) ²

= a⁴ − 2a²b² + b⁴

Area of the remaining part of the farm = Total area of the farm − Area of the square plot

= (2a⁴ + 5a²b² + 3b⁴) − (a⁴ − 2a²b² + b⁴)

= 2a⁴ + 5a²b² + 3b⁴ − a⁴ − 2a²b² + b⁴

= 2a⁴ − a⁴ + 5a²b² + 2a²b² + 3b⁴ − b⁴

= a⁴ + 7a²b² + 2b⁴

Answer is : The area of the remaining part of the farm is (a⁴ + 7a²b² + 2b⁴) sq. meter.

Synthetic Division:

Dividend = 2m² −3m + 10

Divisor = m – 5, Opposite of −5 = 5

The coefficient form of the quotient is (2, 7).

∴ Quotient = 2m + 7 and Remainder = 45

Linear Method:

2m² −3m + 10

= 2m(m − 5) + 10m − 3m + 10

= 2m(m − 5) + 7(m − 5) + 35 + 10

= (m − 5) × (2m + 7) + 45

Answer is : The quotient is 2m + 7 and remainder is 45.

Synthetic division : The coefficient

form of the dividend x⁴ + 2x³ + 3x² + 4x + 5 is (1, 2, 3, 4, 5).

The divisor is x + 2. Opposite of 2 is − 2.

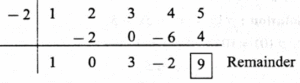
The coefficient form of the quotient is (1, 0, 3, −2).

∴ the quotient = x³ + 3x − 2.

Answer is : The quotient is x³ + 3x − 2 and the remainder is 9.

Linear Method :

x⁴ + 2x³ + 3x² + 4x + 5

= x³(x + 2) − 2x³ + 2x³ + 3x² + 4x + 5

= x³(x + 2) + 3x(x + 2) – 6x + 4x + 5

= x³(x + 2) + 3x(x + 2) −2(x + 2) + 4 + 5

= (x + 2)(x³ + 3x − 2) + 9

Answer is : The quotient is x³ + 3x − 2 and remainder is 9.

Synthetic division : First we write the index form of the dividend.

The index form is y³ + 0y² + 0y − 216.

The coefficient form is (1, 0, 0, − 216)

The divisor is y − 6. Opposite of − 6 is 6.

The coefficient form of the quotient is (1, 6, 36).

∴ the quotient = y² + 6y + 36.

Answer is : The quotient is y² + 6y + 36 and the remainder is 0.

Linear Method :

y³ – 216 = y²(y − 6) + 6y² − 216

= y²(y − 6) + 6y(y − 6) + 36y − 216

= y²(y − 6) + 6y(y − 6) + 36(y − 6) + 216 − 216

= (y − 6) (y² + 6y + 36).

Answer is : The quotient is y² + 6y + 36 and the remainder is 0.

Synthetic division : First we write the standard form of the dividend.

The standard form is 2x⁴ + 3x³ − 2x² + 4x.

The index form is 2x⁴ + 3x³ − 2x² + 4x + 0.

The coefficient form is (2, 3, − 2, 4, 0).

The divisor is x + 3. Opposite of 3 is − 3.

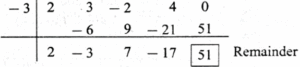
The coefficient form of the quotient is (2, −3, 7, − 17).

∴ the quotient = 2x³ − 3x² + 7x − 17.

Answer is : The quotient is 2x³ − 3x² + 7x – 17 and the remainder is 51.

Linear Method :

2x⁴ + 3x³ + 4x− 2x²

= 2x⁴ + 3x³ − 2x² + 4x

= 2x³(x + 3) − 6x³ + 3x³ − 2r2 + 4r

= 2x³(x + 3) − 3x²(x + 3) + 9x² − 2x² + 4x

= 2x³(x + 3) − 3x²(x + 3) + 7x(x + 3) − 21x + 4x

= 2x³(x + 3) − 3x²(x + 3) + 7x(x + 3) − 17(x + 3) + 51

= (x + 3)(2x³ − 3x² + 7x − 17) + 51.

Answer is : The quotient is 2x³ − 3x² + 7x – 17 and the remainder is 51.

Synthetic division : First we write the index form of the dividend.

The index form is x⁴ + 0x³ − 3x² + 0x − 8.

The coefficient form is (1, 0, − 3, 0, − 8).

The divisor is x + 4. Opposite of 4 is − 4.

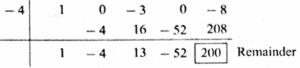
The coefficient form of the quotient is (1, −4, 13, − 52).

∴ the quotient = x³ − 4x² + 13x − 52.

Answer is : The quotient is x³ − 4x² + 13x − 52 and the remainder is 200.

Linear Method :

x⁴ − 3x² − 8

= x³(x + 4) − 4x³ − 3x² − 8

= x³(x + 4) − 4x²(x + 4) + 16x² − 3x² − 8

= x³(x + 4) − 4x²(x + 4) + 13x(x + 4) − 52x − 8

= x³(x + 4) − 4x²(x + 4) + 13x(x + 4) − 52(x + 4) + 208 − 8

= (x + 4)(x³ − 4x² + 13x − 52) + 200.

Answer is : The quotient is x³ − 4x² + 13x − 52 and the remainder is 200.

Synthetic division :

The coefficient form of the dividend y³ − 3y² + 5y − 1 is (1, −3, 5, −1).

The divisor is y − 1. Opposite of − 1 is 1.

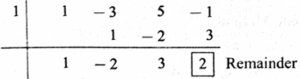
The coefficient form of the quotient is (1, −2, 3).

∴ the quotient = y² − 2y + 3.

Answer is : The quotient is y² − 2y + 3 and the remainder is 2.

Linear Method :

y³ − 3y² + 5y − 1

= y²(y − 1) + y²− 3y² + 5y − 1

= y²(y − 1) − 2y(y − 1) − 2y + 5y − 1

= y²(y − 1) − 2y(y − 1) + 3(y − 1) + 3 – 1

= y²(y − 1) − 2y(y − 1) + 3(y − 1) + 2

= (y − 1)(y² − 2y + 3) + 2.

Answer is : The quotient is y² − 2y + 3 and the remainder is 2.

p (x) = x² − 5x + 5

∴ p(0) = (0)² − 5(0) + 5

= 0 – 0 + 5 = 5

p(0) = 5.

p (y) = y² − 3\(\sqrt{2}\)y + 1

∴ p(3 ) = (3\(\sqrt{2}\))² – 3\(\sqrt{2}\) x 3  + 1

= 9 × 2 – 9 × 2 + 1

= 18 – 18 + 1 = 1

p(3\(\sqrt{2}\)) = 1.

p(m) = m³ + 2m² − m + 10

∴ p(a) = a³ + 2a² − a + 10 and

p(−a) = (−a)³ + 2(−a)² − (−a) + 10

= −a³ + 2a² + a + 10

∴ p(a) + p(−a)

= a³ + 2a² − a + 10 − −a³ + 2a² + a + 10

= 4a² + 20

p(a) + p(−a) = 4a² + 20.

p(y) = 2y³ − 6y² − 5y + 7

∴ p(2) = 2(2)³ − 6(2)² − 5(2) + 7

=2 × 8 – 6 × 4 – 10 + 7

= 16 – 24 – 10 + 7

= − 11

p(2) = − 11.

p(x) = 2x − 2x³ +7

∴ p(3) = 2(3) − 2(3)³ + 7

= 6 – 2 × 27 + 7

= 6 – 54 + 7

= 13 − 54 = − 41

Answer is : The value of the given polynomial for x = 3 is − 41.

p(x) = 2x − 2x³ + 7

∴ p(−1) = 2x(−1) − 2(−1)³ + 7

= − 2 – 2 × (−1) + 7

= − 2 + 2 + 7 = 7

Answer is : The value of the given polynomial for x = −1 is 7.

p(x) = 2x − 2x³ + 7

∴ p(0) = 2(0) − 2(0)³ + 7

= 0 − 2(0) + 7

= 0 – 0 + 7 = 7

Answer is : The value of the given polynomial for x = 0 is 7.

p (m) = m³ + 2m + a

∴ p(2) = (2)³ + 2(2) + a

∴ 12 = 8 + 4 + a       ... [Given, p(2) = 12]

∴ 8 + 4 + a = 12

∴ a = 12 – 8 – 4 = 0

The value of a is 0.

p(x) = mx² − 2x + 3

∴ p(−1) = m(−1)² − 2(−1) + 3     ... [Given, p (−1) = 7]

∴ 7 = m(1) + 2 + 3

∴ 7 = m + 5

∴ m = 7 – 5 = 2

Answer is : m = 2.

p(x) = x²− 7x + 9 divisor = x + 1

∴ take x = − 1

p(−1) = (−1)² − 7(−1) + 9

= 1 + 7 + 9 = 17

Answer is :  The remainder is 17.

p(x) = 2x³ − 2x² + ax − a; divisor = x − a

∴ take x = a

p(a) = 2(a)³ − 2(a)² + a(a)  −a

= 2a³ − 2a² + a² – a

= 2a³ − a² − a

Answer is : The remainder is 2a³ − a² − a.

p(m) = 54m³ + 18m² − 27m + 5; divisor = m − 3

∴ take m = 3

p(3) = 54(3)³ + 18(3)² − 27(3) + 5

= 54(27) + 18(9) − 81 + 5

= 1458 + 162 – 81 + 5

=1625 − 81

= 1544

Answer is : The remainder is 1544.

p(y) = y³ − 5y² + 7y + m; divisor = y + 2

∴ take y = − 2

p(−2) = (−2)³ − 5(−2)² + 7(−2) + m

∴ 50 = − 8 − 5(4) − 14 + m    ... (Given the remainder is 50)

∴ 50 = − 8 – 20 – 14 + m

∴ 50 = − 42 + m

∴ 50 + 42 = m

∴ m = 92

Answer is : The value of m is 92.

By factor theorem, if x + 3 is a factor of the given polynomial, then p(−3) = 0.

p(x) = x² + 2x − 3

∴ p(−3) = (−3)² + 2(−3) − 3

= 9 – 6 − 3

∴ p(−3) = 0

Answer is : (x + 3) is the factor of x² + 2x − 3.

By factor theorem, if (x −2) is a factor of the given polynomial, then p(2) = 0.

p (x) = x³ − mx² + 10x − 20

∴ p(2) = (2)³ − m(2)² + 10(2) − 20

∴ 0 = 8 − 4m + 20 – 20

∴ 4m = 8

∴ m = 2

Answer is : The value of m is 2.

By factor theorem, if q(x) is a factor of p(x), then p(x) = 0.

(i) p (x) = x³ − x² − x − 1; divisor = q(x) = x − 1

∴ take x = 1.

p(1) = (1)³ − (1)² – 1 − 1

= 1 – 1 – 1 – 1 = −2

∴ p(1) = − 2 ∴ p(1) ≠ 0

Answer is : q(x) = (x −1) is not a factor of p(x).

p(x) = 2x³ − x² − 45 divisor = q(x) = x − 3

∴ take x = 3

p(3) = 2(3)³ − (3)² − 45

= 2(27) – 9 − 45

= 54 – 54 = 0

Answer is : g(x) = x − 3 is a factor of p (x).

Dividend polynomial p(x) = x³¹ + 31; divisor = (x + 1)

∴ by remainder theorem, take x = − 1  …(Opposite of + 1)

p(x) = x³¹ + 31

∴ p(−1) = (−1)³¹ + 31

= − 1 + 31 = 30

∴ p(−1) = 30.

Answer is : The remainder is 30.

p(m) = m²¹ − 1; divisor = m − 1.

∴ by the factor theorem, take m = 1.

p(m) = m²¹ − 1

∴ p(1) = (1)²¹ – 1 = 1 – 1 = 0   ... (1)

p(m) = m²² − 1; divisor= m − 1

∴ take m = 1

p(m) = m²² − 1

∴ p(1) = 1²² – 1 = 1 – 1 = 0   ... (1)

(m − 1) is a factor of m²¹ − 1 and m²² − 1.     ∴ [From (1) and (2)]

p (x) = nx² − 5x + m; x − 2 is a factor of nx² − 5x + m.

By factor theorem, p(2) = 0.

∴ p(2) = n(2)² − 5(2) + m = 0

∴ 4n – 10 + m = 0     ... (1)

Also, x – \(\frac{1}{2}\) is a factor of nx² − 5x + m.

By factor theorem, p\((\frac{1}{2})\) = 0

p\((\frac{1}{2})\) = n\((\frac{1}{2})^2\) − 5\((\frac{1}{2})\) + m = 0

\(\frac{n}{4}-\frac{5}{2}\) + m = 0

∴ n – 10 + 4m = 0 ... (Multiplying both the sides by 4)  ... (2)

From (1) and (2),

4n – 10 + m = n – 10 + 4m

∴ 4n – n = 4m − m ∴ 3n = 3m

∴ n = m.    ... (3)

Substituting n = m in equation (1),

4m – 10 + m = 0 ∴ 5m = 10 ∴ m = 2 ... (4)

From (3) and (4), m = n = 2.

p (x) = 2 + 5x

∴ p(2) = 2 + 5(2) = 2 + 10 = 12       ... (1)

p(−2) = 2 + 5(−2) = 2 − 10 = − 8       ... (2)

p(1) = 2 + 5(1) = 2 + 5 = 7       ... (3)

∴ p (2) + p(−2) − p (1) = 12 – 8 – 7 =− 3

Answer is : p(2) + p(−2) − p(1) = −3.

p(x) = 2x² − 5 x + 5.

p(5\(\sqrt{3}\)) = 2(5\(\sqrt{3}\))²− 5 (5\(\sqrt{3}\)) + 5

= 2(25 × 3) − (25 × 3) + 5

= 25 × 3 + 5

= 75 + 5 = 80

Answer is : p(5\(\sqrt{3}\)) = 80.

2x² + x − 1

= 2x² + 2x – x − 1

= 2x(x + 1) −1(x + 1)

= (x + 1)(2x − 1)

Answer is : (x + 1)(2x − 1).

2m² + 5m − 3

= 2m² + 6m – m − 3

= 2m(m + 3) − 1(m + 3)

= (m + 3)(2m − 1)

Answer is : (m + 3)(2m − 1).

12x² + 61x + 77

= 12x² + 28x + 33x + 77                               [12 × 77 = 4 × 3 × 11 × 7

= 4x(3x + 7) + 11(3x + 7)                             = 28 × 33 …(28 + 33 = 61)]

= (3x + 7)(4x + 11)                                      

Answer is : (3x + 7)(4x + 11).

= 3y² − 3y + y − 1

= 3y(y − 1) + 1(y − 1)

= (y − 1)(3y + 1)

Answer is : (y − 1)(3y + 1).

\(\sqrt{3}\)x² + 4x + \(\sqrt{3}\)

= \(\sqrt{3}\)x² + 3x + 1x + \(\sqrt{3}\)                      [ \(\sqrt{3}\) x \(\sqrt{3}\)  = 3,   3 × 1 = 3    ..(3 + 1 = 4)]

= \(\sqrt{3}\)x(x + \(\sqrt{3}\)) + 1(x + \(\sqrt{3}\))              

= (x + \(\sqrt{3}\))( x + 1)

Answer is : (x + \(\sqrt{3}\) )( x + 1).

\(\frac{1}{2}\)x² − 3x + 4

= \(\frac{1}{2}\)(x² − 6x + 8)

= \(\frac{1}{2}\)(x² − 4x – 2x + 8)

= \(\frac{1}{2}\)[x(x − 4) − 2(x − 4)]

= \(\frac{1}{2}\)(x − 4)(x − 2)

Answer is : \(\frac{1}{2}\)(x − 4)(x − 2)

(x² − x)² − 8(x² − x) + 12

= m² − 8m+ 12                     ... [Substituting m for (x² − x)]

= m² − 2m − 6m + 12

= m(m − 2) − 6(m − 2)

= (m − 2)(m − 6)

= (x² – x − 2)(x² −x − 6)         ... [Substituting (x2 − x) for m]

= (x² − 2x + x − 2)(x² − 3x + 2x − 6)

= [x(x − 2) + 1(x − 2)][x(x − 3) + 2(x − 3)]

= (x − 2)(x + 1)(x − 3)(x + 2)

Answer is : (x − 2)(x + 1)(x − 3)(x + 2).

(x − 5)² − (5x − 25) – 24

= (x − 5)² − 5(x − 5) − 24

= m² − 5m − 24                     ... [Substituting m for (x − 5)]

= m² − 8m + 3m − 24

= m(m − 8) + 3(m − 8)

= (m − 8)(m + 3)

= (x − 5 − 8)(x − 5 + 3)         ... [Substituting (x − 5) for m]

= (x − 13)(x − 2)

Answer is : (x − 13)(x − 2).

(x² − 6x)² − 8 (x² − 6x +8) − 64       ... (Let x² − 6x = m)

= m² −8(m + 8) − 64

= m² − 8m – 64 − 64

= m² − 8m − 128

= m² − 16m + 8m − 128

= m(m − 16) + 8(m − 16)

= (m − 16)(m + 8)

= (x² − 6x − 16)(x² − 6x + 8) ... [m = x² − 6x]

= (x² − 8x + 2x − 16)(x² − 4x − 2x + 8)

= [x(x − 8) + 2(x − 8)][x(x − 4) − 2(x − 4)]

= [(x − 8)(x + 2)][(x − 4)(x − 2)]

= (x − 8)(x + 2)(x − 4)(x − 2)

Answer is : (x − 8)(x + 2)(x − 4)(x − 2).

(x² − 2x + 3) (x² − 2x + 5) – 35

= (m + 3)(m + 5) − 35          ... (Let x² − 2x = m)

= m(m + 5) + 3(m + 5) − 35

= m² + 5m + 3m + 15 − 35

= m² + 8m − 20

= m² + 10m − 2m − 20

= m(m + 10) − 2(m + 10)

= (m + 10)(m − 2)

= (x² − 2x + 10)(x² − 2x − 2)          ... [m = x² − 2x]

Answer is : (x² − 2x + 10)(x² − 2x − 2).

(y + 2) (y − 3)(y + 8)(y + 3) + 56

= (y + 2)(y + 3)(y − 3)(y + 8) + 56

= [y(y + 3) + 2(y + 3)][y(y + 8) − 3(y + 8)] + 56

= (y² + 3y + 2y + 6)(y² + 8y − 3y − 24) + 56

= (y² + 5y + 6)( y² + 5y − 24) + 56

= (x + 6)(x − 24) + 56 ... (Let y² + 5y = x)

= x(x − 24) + 6(x − 24) + 56

= x² − 24x + 6x – 144 + 56

= x² − 18x − 88

= x² − 22x + 4x − 88

= x(x − 22) + 4(x − 22)

= (x − 22)(x + 4)

= (y² + 5y − 22)(y² + 5y + 4)        ... [x = y² + 5y]

= (y² + 5y − 22)(y² + 4y + y + 4)

= (y² + 5y − 22)[y(y + 4) + 1(y + 4)]

= (y² + 5y − 22)(y + 4)(y + 1)

Answer is : (y² + 5y − 22)(y + 4)(y + 1).

(y² + 5y)(y² + 5y − 2) – 24

=(n)(n − 2) − 24           ... (Let y² + 5y = n)

= n² − 2n − 24

= n² − 6n + 4n − 24

= n(n − 6) + 4(n − 6) = (n − 6)(n + 4)

= (y² + 5y − 6)(y² + 5y + 4) ... [n = y² + 5y]

= (y² + 6y – y − 6)(y² + 4y + y + 4)

= [y(y + 6) −1(y + 6)][y(y + 4) + 1(y + 4)]

= [(y + 6)(y − 1)][(y + 4)(y + 1)]

= (y + 6)(y − 1)(y + 4)(y + 1)

Answer is : (y + 6)(y − 1)(y + 4)(y + 1).

(x − 3)(x − 4)²(x − 5) – 6

= [(x − 3)(x − 5)](x − 4)² − 6

= [x(x − 5) − 3(x − 5)](x² − 8x + 16) − 6

= [x² − 5x − 3x + 15](x² − 8x + 16) − 6

= (x² − 8x + 15)(x² − 8x + 16) − 6

= (m + 15)(m + 16) − 6        ... (Let x² − 8x = m)

= m(m + 16) + 15(m + 16) − 6

= m²+ 16m + 15m + 240 − 6

= m² + 31m + 234

= m² + 18m + 13m + 234

= m(m + 18) + 13(m + 18)

= (m + 18)(m + 13)

= (x² − 8x + 18)(x² − 8x + 13)        ... [m = x² – 8x]

Answer is : (x² − 8x + 18)(x² − 8x + 13).

(D) \(\sqrt{2}\)x² + \(\frac{1}{2}\)

(In the other three, the powers of variables are not positive integers.)

(D) 0

(\(\sqrt{7}\) = \(\sqrt{7}\)x°. ∴ the degree is zero.)

(C) undefined : [As per definition]

(A) 3 : (The highest degree is 3.)

(C) (1, 0, 0, − 1)

[x³ – 1 = x3 + 0x2 + 0x −1 ... (Index form)

∴ coefficient form is (1, 0, 0, −1)]

(A) 3

[x² − 7\(\sqrt{7}\)x + 3

∴ p (7\(\sqrt{7}\)) = (7\(\sqrt{7}\))² − 7 (7\(\sqrt{7}\)) + 3 = 49 × 7 – 49 × 7 + 3 = 3.]

(D) – 4

(C) − 3

[By remainder theorem,

3x² + mx = 3(1)² + m(1) = 3 + m = 0

∴ m = − 3]

(A) 5

[(x² − 3)(2x − 7x³ + 4) = x² x x³ = x⁵

∴ degree of the product is 5]

(A) x + 5

[(x + 5) is a linear polynomial with degree 1.]

(i) The degree is 4

(ii) The degree is 0

(iii) The degree is 9.

7x⁴ − x³ + 4x² − x + 9

5p⁴ + 2p³ + 10p² + p − 8.

(i) x⁴ + 16 = x⁴ + 0x³ + 0x² + 0x + 16            ... (Index form)

∴ the coefficient form is (1, 0, 0, 0, 16).

m⁵ + 2m² + 3m + 15

= m⁵ + 0m⁴ + 0m³ + 2m² + 3m + 15              ... (Index form)

∴ the coefficient form is (1, 0, 0, 2, 3, 15).

The number of coefficients = 5.

∴ the degree of the polynomial = 5 − 1 = 4.

The index form : 3x⁴ – 2x³ + 0x² + 7x + 18.

The number of coefficients = 4.

∴ the degree of the polynomial = 4 − 1 = 3.

The index form : 6x³ + x² + 0x + 7.

The number of coefficients = 4.

∴ the degree of the polynomial = 4 − 1 = 3.

The index form : 4x³ + 5x² − 3x + 0.

(7x⁴ − 2x³ + x + 10) + (3x⁴ + 15x³ + 9x² − 8x + 2)

= 7x⁴ − 2x³ + x + 10 + 3x⁴ + 15x³ + 9x² − 8x + 2

= 7x⁴ + 3x⁴ − 2x³ + 15x³ + 9x² + x − 8x + 10 + 2              ... (Collecting like terms)

= 10x⁴ + 13x³ + 9x² − 7x +12

Answer is : 10x⁴ + 13x³ + 9x² − 7x +12.

(3p³q + 2p²q + 7) + (2p²q + 4pq − 2p³q)

= 3p³q + 2p²q + 7 + 2p²q + 4pq − 2p³q

= 3p³q − 2p³q + 2p²q + 2p²q + 4pq + 7                            ... (Collecting like terms)

= p³q + 4p²q + 4pq + 7.

Answer is : p³q + 4p²q + 4pq + 7.

Question 7. Subtract the second polynomial from the first.

(i) 5x² − 2y + 9 ; 3x² + 5y − 7

(5x² − 2y + 9) − (3x² + 5y − 7)

= 5x² − 2y + 9 − 3x² − 5y + 7

= 5x² − 3x² −2y − 5y + 9 + 7                   ... (Collecting like terms)

= 2x² − 7y + 16

Answer is : 2x² − 7y + 16

(ii) 2x² + 3x + 5 ; x² − 2x + 3

(2x² + 3x + 5) − (x² − 2x + 3)

= 2x² + 3x + 5 − x² + 2x − 3

= 2x² − x² + 3x + 2x + 5 – 3                  ... (Collecting like terms)

= x² + 5x + 2.

Answer is : x² + 5x + 2

Question 8. Multiply the following polynomials.

(i) (m³ − 2m + 3)(m⁴ − 2m² + 3m + 2)

(m³ − 2m + 3)( m⁴ − 2m² + 3m + 2)

= m³(m⁴ − 2m² + 3m + 2) − 2m(m⁴ − 2m² + 3m + 2) + 3(m⁴ − 2m² + 3m + 2)

=m⁷ − 2m⁵ + 3m⁴ + 2m³ − 2m⁵ + 4m³ − 6m² − 4m + 3m⁴ − 6m² + 9m + 6

= m⁷ − 2m⁵ − 2m⁵ + 3m⁴ + 3m⁴ + 2m³ + 4m³ − 6m² − 6m² − 4m + 9m + 6

= m⁷ − 4m⁵ + 6m⁴ + 6m³ − 12m² + 5m + 6

Answer is : m⁷ − 4m⁵ + 6m⁴ + 6m³ − 12m² + 5m + 6.

(ii) (5m³ − 2)(m² − m + 3)

(5m³ − 2)( m² − m + 3)

= 5m³(m² – m + 3) − 2(m² – m + 3)

= 5m⁵ − 5m⁴ + 15m³ − 2m² + 2m − 6

Answer is : 5m⁵ − 5m⁴ + 15m³ − 2m² + 2m − 6.

Question 9. Divide polynomial 3x³ − 8x² + x + 7 by x − 3 using synthetic method and write the quotient and remainder.

Dividend = 3x³ − 8x² + x + 7

Its coefficient form : (3, −8. 1, 7)

Divisor = x – 3. Opposite of − 3 is 3.

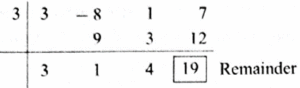
The coefficient form of quotient = (3, 1, 4)

Answer is : The quotient = 3x² + x + 4; remainder = 19.

Question 10. For which the value of m, x + 3 is the factor of the polynomial x³ − 2mx + 21 ?

(x + 3) is a factor of

p (x) = x³ − 2mx + 21.

∴ by factor theorem, p (−3) = 0.

p (x) = x³ − 2mx + 21.

∴ p(−3) = (−3)³ − 2m(−3) + 21

∴ 0 = − 27 + 6m + 21

∴ 0 = − 6 + 6m  ∴ 6 = 6m  ∴ m = 1

Answer is : For the value of m = 1.

Question 11. At the end of the year 2016, the population of villages Kovad, Varud, Chikhali is 5x² − 3y², 7y² + 2xy and 9x² + 4xy respectively. At the beginning of the year 2017, x² + xy − y², 5xy and 3x² + xy persons from each of the three villages respectively went to another village for education then what is the remaining total population of these three villages ?

Total population of the three villages

= (5x² − 3y²) + (7y² + 2xy) + (9x² + 4xy)

= 5x² − 3y² + 7y² + 2xy + 9x² + 4xy

= 5x² + 9x² − 3y² + 7y² + 2xy + 4xy

= 14x² + 4y² + 6xy

Total number of persons who went to another village for education

= (x² + xy − y²) + 5xy + (3x² + xy)

= x² + xy − y² + 5xy + 3x² + xy

= x² + 3x² − y² + xy + 5xy + xy

= 4x² − y² + 7xy

∴ Remaining total population of the three villages = Total population of the three villages − Total number of persons who went to another village for education

= (14x² + 4y² + 6xy) − (4x² − y2 + 7xy)

= 14x² + 4y² + 6xy − 4x² + y² − 7xy

= 14x² − 4x² + 4y² + y² + 6xy − 7xy

= 10x² + 5y² − xy

Answer is : The remaining total population of these three villages is 10x² + 5y² – xy.

Question 12. Polynomials bx² + x + 5 and bx3 − 2x + 5 are divided by polynomial x − 3 and the remainders are m and n respectively. If m − n = 0 then find the value of b.

Let p(x) = bx² + x + 5 and q(x) = bx³ − 2x + 5.

The remainder when p(x) = bx² + x + 5 is divided by (x − 3) is m.

By remainder theorem,

Remainder = p(3) = m

∴ b(3)² + 3 + 5 = m

∴ m = 9b + 8              ... (1)

The remainder when q(x) = bx³ − 2x + 5 is divided by (x − 3) is n.

By remainder theorem,

Remainder= q(3) = n

∴ b(3)³ −2(3) + 5 = n

∴ n = 27b – 6 + 5 = 27b – 1  ... (2)

Now,

m – n = 0

(9b + 8) − (27b − 1) = 0   ….[Using (1) and (2)]

9b − 27b + 8 + 1 = 0

= − 18b + 9 = 0

− 18b = − 9

b = \(\frac{-9}{-18}=\frac{1}{2}\)

Answer is : The value of b is \(\frac{1}{2}\)

Question 13. Simplify. (8m² + 3m − 6) − (9m − 7) + (3m² − 2m + 4)

(8m² + 3m − 6) − (9m − 7) + (3m² − 2m + 4)

= 8m² + 3m – 6 − 9m + 7 + 3m² − 2m + 4

= 8m² + 3m² + 3m − 9m − 2m – 6 + 7 + 4

= 11m² − 8m + 5

Answer is : 11m² − 8m + 5

Let p(x) be the polynomial which is to be subtracted from x² + 13x + 7 to get the polynomial 3x² + 5x − 4.

∴ (x² + 13x + 7) − p(x) = 3x² + 5x − 4

p(x) = (x² + 13x + 7) − (3x² + 5x − 4)

p(x) = x² + 13x + 7 − 3x² − 5x + 4

p(x) = x² − 3x² + 13x − 5x + 7 + 4

= p(x) = − 2x² + 8x + 11

Answer is : The required polynomial is −2x² + 8x + 11.

The required polynomial can be obtained by subtracting the polynomial 4m + 2n + 3 from 6m + 3n + 10.

∴ Required polynomial

∴ (4m + 2n + 3) + p(a) = (6m + 3n + 10)

∴ p(a) = (6m + 3n + 10) − (4m + 2n + 3)

= 6m + 3n + 10 − 4m − 2n − 3

= 6m − 4m + 3n − 2n + 10 − 3

= 2m + n + 7

Thus, the polynomial 2m + n + 7 is to be added to 4m + 2n + 3 to get the polynomial 6m + 3n + 10.