Topics to be learn : Gravitation Free Fall Mass Weight Thrust and Pressure Archimedes’ Principle

Gravitational force: There exists a force of attraction between any two particles of matter in the universe such that the force depends only on the masses of the particles and the separation between them. It is called the gravitational force and the mutual attraction is called gravitation.

• Example : The gravitational force between the earth and the moon.
• The gravitational force is a universal force, i.e., it acts between any two objects in the universe.

Gravitation :

Gravitation is defined as the force of attraction between any two bodies in the universe.

Example : The earth attracts (or pulls) all objects lying on or near its surface towards its centre.

• The force with which the earth pulls the objects towards its centre is called the gravitational force of the earth or gravity of the earth.

Universal Law Of Gravitation

Newton's universal law of gravitation : Every object in the Universe attracts every other object with a definite force. This force is directly proportional to the product of the masses of the two objects and inversely proportional to the square of the distance between them.

• As the law of gravitation given by Newton is applicable throughout the universe and to all particles. Hence it is called universal law.

Consider two objects of masses m₁ and m₂. We assume that the objects are very small spheres of uniform density and the distance r between their centres is very large compared to the radii of the spheres (Fig.).

The magnitude (F) of the gravitational force of attraction between the objects is directly proportional to m₁m₂ and inversely proportional to r²

F ∝ \(\frac{m_1m_2}{r^2}\)  ∴ F = G\(\frac{m_1m_2}{r^2}\)

where, G = 6.67x 10^-11 N-m²/kg² is called the universal gravitational constant.

• The above law means that if the mass of one object is doubled, the force between the two objects also doubles. Also, if the distance is doubled, the force decreases by \(\frac{1}{4}\).
• Its value does not depend on the medium between the two bodies and the masses of the bodies or the distance between them. Suppose the masses of two bodies are 1 kg each and the distance r between them is 1 m, then

F = G       …..[∵ m₁ = m₂ = 1 kg and r = 1 m]

Hence, the universal gravitational constant is defined as the gravitational force between two bodies of unit masses separated by a unit distance from each other and placed anywhere in space. The SI unit of G is N-m²kg^-2 .

• The value of G was found out by Henry Cavendish (1731-1810) by using a sensitive balance.
• According to third law of motion, an object like apple does not attract the earth because the mass of an apple is negligibly small compared to that of earth.
• Universal law of gravitation is universal in the sense that it is applicable to all bodies, whether the bodies are big or small whether they are terrestrial.

Importance of the Universal Law of Gravitation :

This law explains successfully, i.e., with great accuracy,

• the force that binds the objects on the earth to the earth
• the motion of the moon and artificial satellites around the earth
• the motion of the planets, asteroids, comets, etc., around the Sun
• the tides of the sea due to the moon and the Sun.

Motion of Moon Around Earth and Centripetal Force :

The force that keeps a body moving along the circular path acting towards the centre is called centripetal (centre seeking) force. This force is responsible for changing the direction and velocity of an object.

The motion of the moon around the earth is due to the centripetal force. The centripetal force is provided by the gravitational force of attraction of the earth.

If there were no such force, then the moon would pursue a uniform straight line motion.

Note : A straight line that meets the circle at one and only one point is called a tangent to the circle. In figure, A-B-C represents the tangent to circle.

Free Fall :

When objects fall towards the earth under the influence of earth's gravitational force alone, then these objects are called freely falling objects and such motion is called free fall.

Acceleration due to Gravity (g) :

Whenever an object falls towards the earth, an acceleration is involved. This acceleration is due to the earth's gravitational pull and is called acceleration due to gravity.

• It is denoted by g.
• The SI unit of g is the same as that of acceleration, i.e. m/s²

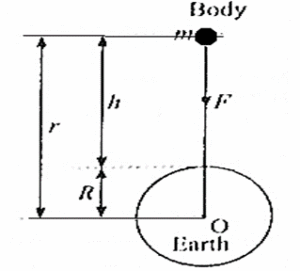
Suppose that a body of mass m is released from a distance r from the centre (O) of the earth.

Let M be the mass of the earth. According to newton’s law of the gravitation the magnitude of the earth’s gravitational force acting on the body is

F= G\(\frac{Mm}{r^2}\)

Where G is the universal constant of gravitation

The acceleration produced by this force,

g = Force/mass = F/m

∴ g = \(\frac{GM}{r^2}\)

This is the formula for the acceleration due to gravity or the gravitational acceleration due to the earth. This acceleration is directed towards the earth's centre.

If h denotes the altitude, r = R + h, where R is the radius of the earth.

∴ g = \(\frac{GM}{(R+h)^2}\)

For a body on the earth's surface, h = 0,  g = \(\frac{GM}{R^2}\)

[For r ≥ R (radius of the earth).  It depends on the location of the body.]

To Calculate the Value of g :

To calculate the value of g, we should put the values of G, M and R in above formula, i.e. g = \(\frac{GM}{r^2}\)

Mass of the earth, M = 6 x 10²⁴ kg

Radius of the earth, R = 6.4 x 10⁶ m

Universal gravitational constant, G = 6.67 × 10^-11 N-m²/kg²

g = \(\frac{GM}{r^2}\) = \(\frac{6.67×10^{-11}×6×10^{24}}{(6.4×10^6)^2}\)

g = 9.8 m/s²

Motion of Objects Under the Influence of Gravitational Force of the Earth :

Equations of Motion for Free Fall :

The three equations of motion which we have derived earlier are for bodies under uniform acceleration.

In case of motion of bodies under free fall, there is a uniform acceleration, i.e. acceleration due to gravity (g) acting downward.

So, the previous three equations of motion can be applied for the motion of bodies under free fall as follows

General equations of motion	Equations for body under free fall
v = u + at	v = u + gt           [∵ a = g]
s = ut + \(\frac{1}{2}\)at2	h = ut + \(\frac{1}{2}\)gt2      [∵ a = g]
v2 = u2 + 2as	v2 = u2 + 2gh      [∵ a = g]

where, h is the height from which the object falls, t is the time of fall, u is the initial velocity and v is the final velocity when the body accelerates at g.

In solving numerical problems, we should remember the following points

• If an object falls vertically downwards, then acceleration due to gravity is taken as positive, since its velocity increases while falling.
• If an object is thrown vertically upwards, then acceleration due to gravity is taken as negative, since its velocity decreases as it moves upward.

Mass :

It is the total content of the body which measures the inertia of a body. In other words, mass is the quantity of matter contained in a body.

• It is a scalar quantity and its SI unit is kilogram.
• Irrespective of the position of the body in the universe, mass always remains constant everywhere. The mass of the body cannot be zero.
• The centre of mass of a body may be defined as the point at which whole mass of the body may be assumed or concentrated.

Weight :

The weight of an object is the force with which it is attracted towards the earth. It is denoted by w.

We know that,

F = m x a

i.e. F = m x g      ….(i)

The force of attraction of the earth on an object is known as the weight of the object.

Substituting the same in Eq. (i), we get

Weight of an object, w = mg

where, m = mass and g = acceleration due to gravity.

Or w = \(\frac{GMm}{R^2}\)

Here, M = mass of the earth and R = radius of the earth.

Weight of an Object on the Moon :

The weight of an object on the moon is the force with which the moon attracts the object.

The moon exerts lesser force of attraction on objects than that of earth because the mass of moon is less than that of the earth.

Let the mass of an object be m and its weight on the moon be w_m. Suppose the mass of the moon is M_m and its radius be R_m. According to universal law of gravitation, the weight of an object on the moon will be

w_m = \(\frac{GM_mm}{R_m^2}\)             ….(i)

Let the weight of the same object on the earth be w_e, mass of the earth be M_e and the radius of the earth be R_e.

w_e = \(\frac{GM_em}{R_e^2}\)              ….(ii)

From Eqs. (i) and (ii), we have

\(\frac{w_m}{w_e}\) = \(\frac{\frac{GM_mm}{R_m^2}}{\frac{GM_em}{R_e^2}}\) = \(\frac{M_mR_e^2}{M_eR_m^2}\)

Now, M_m = 5.98 x 10²¹ kg, M_e = 7.36 x 10²² kg

R_m = 1.74 x 10⁶, R_e = 6.37 × 10⁶

\(\frac{w_m}{w_e}\) = \(\frac{5.98×10^{21}×(6.37×10^6)^2}{7.36×10^{21}×(1.74×10^6)^2}\) = \(\frac{1}{6}\)

Thus, the weight of an object on the moon is one-sixth of its weight on the earth.

Thrust and Pressure

Thrust : Thrust is the force acting on an object perpendicular to its surface. The effect of thrust depends on the area on which it acts.

• The unit of thrust is the same as that of force, i.e. the SI unit of thrust is newton (N). It is a vector quantity.

Pressure : Pressure is the force acting perpendicularly on a unit area of an object.

Pressure (p) = \(\frac{Force(P)}{Area(A)}\) = \(\frac{Thrust}{Area}\) 

The SI unit of pressure is Nm-2, which is also called pascal (Pa) named after the scientist Blaise Pascal. It is a scalar quantity.

1 Pa = 1 Nm^-2

• From the formula of pressure, it is clear that the same force can produce different pressures depending on the area over which it acts.
• A force acting on a smaller area exerts a large pressure while the same force acting on a larger area exerts a small pressure. This is the reason why a nail has a pointed tip, knives have sharp edges and buildings have wide foundations.

Pressure in Fluids :

All liquids and gases are together called fluids. Water and air are two most common fluids. Solids exert pressure on a surface due to their weight.

Fluids also have weight, therefore fluids also exert pressure on the base and walls of the container in which they are enclosed. Fluids exert pressure in all directions.

Buoyancy :

• The tendency of a liquid to exert an upward force on an object immersed in it is called buoyancy. Gases also exhibit this property of buoyancy.
• Buoyant force is an upward force which acts on an object when it is immersed in a liquid. It is also called upthrust.
• It is the buoyant force due to which a heavy object seems to be lighter in water. As we lower an object into a liquid, the liquid underneath it provides an upward force.

Example : A piece of cork is held below the surface of water. When we apply a force by our thumb, the cork immediately rises to the surface. This is due to the fact that every liquid exerts an upward force on the objects immersed in it.

• An object seems lighter when immersed in liquid. This reduced weight of an object in liquid is called apparent weight of an object.
• The pressure exerted by a liquid increases with depth and acts in all directions.

Why Objects Float or Sink When Placed on the Surface of Water?

When an object is immersed in a liquid, then following two forces act on it

• Weight of the object which acts in downward direction, i.e. it tends to pull down the object.
• Buoyant force (upthrust) which acts in upward direction, i.e. it tends to push up the object.

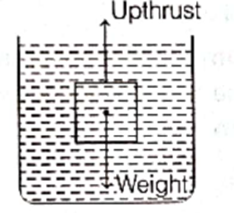
Whether an object will float or sink in a liquid, depends on the relative magnitudes of these two forces which act on the object in opposite directions.

There are three conditions of floating and sinking of objects as given below

• If the buoyant force or upthrust exerted by the liquid is less than the weight of the object, the object will sink in the liquid.
• If the buoyant force is equal to the weight of the object, the object will float in the liquid.
• If the buoyant force is more than the weight of the object, the object will rise in the liquid and then float.

Density :

The density of a substance is defined as mass per unit volume.

Density = \(\frac{\text{Mass of substance}}{\text{Volume of substance}}\)  = or ρ = \(\frac{m}{V}\)

• The SI unit of density is kilogram per metre cube (kg/m³).
• It is a scalar quantity.

The density of a substance under specified conditions always remains same, hence the density of a substance is one of its characteristic properties. It can help us to

determine its purity.

It is different for different substances. The lightness and the heaviness of different substances can be described by using the word density.

Objects having less density than that of a liquid, will float on the liquid. Objects having greater density than that of liquid, will sink in the liquid. The density decreases with increase in temperature.

The object having density equal to that of liquid will float on the liquid in such a way that it is totally submerged in the liquid and no part of it remains above the surface of the liquid.

Archimedes’ Principle

It states that, "when an object is fully or partially immersed in a liquid, it experiences a buoyant force or upthrust, which is equal to the weight of liquid displaced by the object", i.e.

Buoyant force or upthrust acting on an object = Weight of liquid displaced by the object

According to this principle, "an object will float in a liquid, if the weight of object is equal to the weight of liquid displaced by it". This is called law of floatation.

Even gases like air, exert an upward force or buoyant force on the objects placed in them. It is buoyant force or upthrust which makes a balloon rise in air.

Applications of Archimedes' Principle

Archimedes' principle is used in

• designing ships and submarines.
• lactometer (a device used to determine the purity of milk).
• hydrometer (a device used for determining the density of liquid).

Q. How does a Boat Float in Water?