Motion
NCERT-CBSE-Class-9-Science-Chapter-7
Notes
|
Topics to be learn :
|
In everyday life, we observe various motions such as vehicles, birds, watch needles, fan blades, and blood circulation. Atoms, molecules, planets, stars, and galaxies are also in motion.
A body is considered in motion if it changes its position with respect to time and surroundings.
Describing Motion :
Position : The location of an object with respect to a particular point is known as the position of the object. The particular point about which the position of the object is defined is called reference point or origin.
Scalar and Vector Quantities :
- A physical quantity which has only magnitude, i.e. number is called scalar quantity. e.g. mass, time, distance, speed, etc.
- A physical quantity which has magnitude as well as direction is called vector quantity. e.g. weight, displacement, velocity, etc.
Motion Along A Straight Line :
Distance : The distance travelled by a moving body is the actual length of the path
covered by it, irrespective of the direction in which the body travels.
- It is a scalar quantity.
- Its SI unit is metre.
Example : Consider the motion of an object moving along a straight path. Let the object start its motion from point O and move through point A, B, C and reach upto point D.
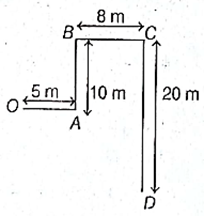
Then, total distance covered to the object = actual length upto D of the path travelled
= OA + AB + BC + CD
= 5m + 10m + 8m + 20m
= 43 m
Displacement : The displacement of an object is the change in the position of the object when it moves from a given position to another position.
It is equal to the length of the shortest path measured in the direction from the initial position to the final position of the object.
- It is a vector quantity.
- Its SI unit is metre (m).
Example : Suppose an object starts to move from point O and reaches to point B, passing through A.
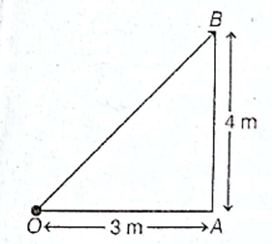
Here, initial position of the object is O and final position is B.
So, displacement of the object = length of the shortest path between initial position (O) and final position (B)
= OB = \(\sqrt{OA^2+AB^2}\) ……..[from Pythagoras theorem]
= \(\sqrt{3^2+4^2}\) = \(\sqrt{25}\) = 5 m
But, distance in this case = length of actual path = OA + AB = 3m + 4m = 7m
Distance versus Displacement :
(i) Displacement of a moving object can never be greater than the distance travelled by it.
∴ Displacement ≤ Distance
∴ \(\frac{Displacement}{Distance}\) ≤ 1, i.e. Ratio of displacement and distance is always less than or equal to 1.
(ii) If a body moves along a straight line (only in one direction), then distance and displacement will be equal.
(iii) Displacement of the object can be positive, negative or zero but distance cannot be negative or zero.
Example : If a car, starting from point P, goes to point Q and then returns to point P (see Fig.), how much distance has it travelled and what is its displacement?
Answer :
The distance travelled by the car = PQ + QP = 360 m + 360 m = 720 m,
its displacement = zero metre.
Uniform Motion And Nonuniform Motion
Uniform Motion : A body is said to have a uniform motion, if it travels equal distances in equal intervals of time. The distance travelled by an object in uniform motion increases linearly.
- Example : A car moving along a straight line path, covers equal distances in equal intervals of time, it is said to be in uniform motion.
Non-uniform Motion : A body is said to have a non-uniform motion, if it travels unequal distances in equal intervals of time.
- Example : A car moving through a crowded market has non-uniform motion.
Measuring the Rate of Motion :
The ratio of distance travelled by an object to the time taken is called rate of motion. The various terms required to measure the rate of motion are as given below.
Speed : Speed is the distance covered by a body in unit time.
Speed = total distance covered / total time taken
- Its SI unit is the metre/second (m/s) and CGS unit is the centimetre/second (cm/s).
- Speed has magnitude, but not direction. It is a scalar quantity.
Speed = distance/time.
∴ Distance = speed x time.
- The speed may be positive or zero but never negative.
Speed can be classified as
(i) Uniform speed : If a moving body does not change its speed during motion, then the speed of the body is said to be uniform, i.e. constant speed.
(ii) Non-uniform speed : If a moving body changes its speed during motion, then the speed of the body is said to be non-uniform, i.e. variable speed.
(iii) Average speed It is defined as the ratio of the total distance travelled by a body to the total time taken.
It is expressed as
Average speed = \(\frac{\text{Total Distance travelled}}{\text{Total time taken}}\)
If a body covers distance s1 in time t1 and then distance s2 in time t2 its average speed over the time (t1 + t2) is vav = \(\frac{s_1+s_2}{t_1+t_2}\)
Instantaneous speed : The speed of an object at any particular instant of time or at a particular point of its path is called the instantaneous speed of the object.
Speed with Direction :
Velocity is the distance covered by a body in a given direction in unit time. Thus, it is the displacement in unit time or the rate at which displacement takes place with respect to time.
It is expressed as
Velocity of an object (v) = \(\frac{Displacement}{Time}\)
- Its SI unit is the metre/second (m/s) and CGS unit is the centimetre/second (cm/s). same as those of speed.
- Velocity has both magnitude and direction. It is a vector quantity.
- It can be positive, zero or negative.
- It can be changed by changing the object's speed, direction of motion or both.
- When a body moves without a change of direction of motion, the magnitude of the velocity of the body equals the speed of the body.
- When there is a change in the direction of motion of a body as the body moves along a curve or follows a zigzag path, the speed of the body is greater than the magnitude of the velocity of the body.
Velocity can be classified as
(i) Uniform velocity : If an object does not change, its velocity during motion without changing direction, then its velocity is known as uniform velocity, i.e. constant velocity.
(ii) Non-uniform velocity : If an object changes its velocity during motion, then its velocity is known as non-uniform velocity, i.e. variable velocity.
(iii) Average velocity : It is defined as the ratio of total displacement of the object to the total time taken.
It is expressed as vav = \(\frac{Total\,displacement}{Time\,taken}\)
If the velocity of an object changes at a uniform rate, then average velocity, vav = \(\frac{\text{Initial velocity(u)+Final velocity(v)}}{2}\)
- Speedometer is a device which is used to measure instantaneous speed of a moving body.
- Average speed of a moving object can never be zero but the average velocity of a moving object can be zero.
Instantaneous velocity : The velocity of an object at a particular instant of time or at a particular point of its path is called its instantaneous velocity.
Rate of Change of Velocity :
Acceleration is defined as the rate of change of velocity with respect to time.
Mathematically, it is expressed as
Acceleration = \(\frac{\text{Change in velocity(Δv)}}{\text{Change in time(Δt)}}\)
If in a given time interval t, the velocity of a body changes from u to v, then acceleration a is expressed as
a = \(\frac{\text{Final velocity(v)-Initial velocity(u)}}{Time}\)
If a body moves in a straight line, its acceleration, a = \(\frac{v-u}{t}\), where u is the initial velocity of the body and v is the velocity of the body after time t. v is often called the final velocity.
This kind of motion is known as accelerated motion.
- The SI unit of acceleration is m/s2. It is a vector quantity.
- The acceleration is taken to be positive, if it is in the direction of velocity, negative if it is opposite to the direction of velocity and zero when a body is moving with a constant velocity.
- If velocity of an object decreases with time, then it is said to have negative acceleration. Negative acceleration is also called deceleration or retardation.
Acceleration can be classified as
(i) Uniform acceleration : If an object travels in a straight line and its velocity increases or decreases by equal amounts in equal intervals of time, then the
object is said to be in a uniform acceleration.
Examples:
- The motion of a freely falling body.
- The motion of a ball rolling down on an inclined plane.
(ii) Non-uniform acceleration : If velocity of an object increases or decreases by unequal amounts in equal intervals of time, then the object is said to be in a
non-uniform acceleration.
Examples:
- The movement of a car on a crowded city road.
- The motion of the train leaving or entering the platform.
Graphical Representation of Motion :
- Line graphs are used to depict the motion of an object, highlighting the dependence of physical quantities like distance or velocity on time.
- Time is taken along the X-axis as an independent variable, while distance, speed, or velocity are taken along the Y-axis as dependent variables.
Types of Graph :
There are two main types of graph which we will be studying as given below.
Distance-Time Graph :
- The change in the position of an object with time can be represented on the distance-time graph by adopting a convenient scale of choice.
- To draw a distance-time graph, time is plotted along X-axis and distance of the body is plotted along Y-axis. In this case, the slope of the distance-time graph is equal to the speed of the object.
- If the distance-time graph is a straight line parallel to time axis, it means the object is at rest.
Distance-time graphs under various conditions are explained below
(i) Distance-Time Graph for Uniform Motion
If an object travels equal distances in equal intervals of time, then it moves with uniform speed. This shows that the distance travelled by the object is directly proportional to the time.
For uniform speed, a graph of distance travelled against time is a straight line as shown in figure given below.
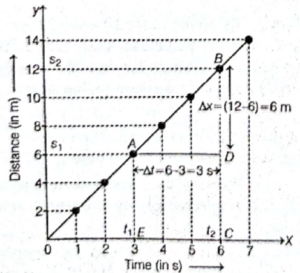
Distance-time graph of an object moving with uniform speed
Interpretation :
From the graph, it is clear that in equal interval of time, i.e. Is, the object covers equal distance 2 m, so the motion is uniform and graph is a straight line.
Calculation of speed : To calculate the speed of the object from a distance-time graph, choose any two points say A and B on the straight line.
From points A and B, draw perpendiculars AE and BC respectively, on time axis. Now, draw a perpendicular AD on BC. The distance travelled by the object from point A to B is given by
Δx = BC - CD = s2 - s1
Time taken by the object to cover this distance
Δt = t2 – t1
∴ Speed, v = Δx/Δt = (s2 - s1)/(t2 – t1)
i.e. Ax/At = Slope of distance-time graph.
(ii) Distance-Time Graph for Non-uniform Motion :
If a body travels unequal distances in equal intervals of time, then the motion of the body is known as non-uniform motion.
Non-uniform motion is of two types such as
(a) When the speed of the body increases with passage of time, then the distance-time graph will be a curve with positive slope as shown below
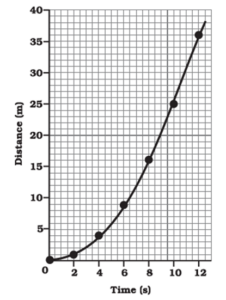
Distance-time graph for a car moving with non-uniform speed
Interpretation
From the graph, it is clear that in equal intervals of time of two seconds, the body is covering unequal distances and this distance goes on increasing. That means, with the passage of time, the body is covering more and more distance in equal time, i.e. the speed of the body is increasing.
(b) When the speed of the body decreases with passage of time, then the distance-time graph will be a curve with negative slope as shown below
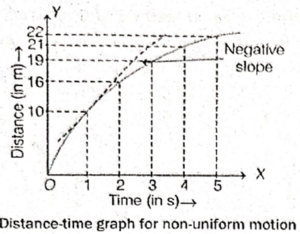
Interpretation :
From the graph, it is clear that in equal intervals of time of one second, the body is covering unequal distances and this distance goes on decreasing. That means, with the time, the body is covering lesser and lesser distance in equal time, i.e. the speed of the body is decreasing.
Velocity-Time Graphs :
Velocity-time graph shows how the velocity of a body changes with passage of time. The slope of velocity-time graph gives the acceleration.
To draw velocity-time graph, velocity of the body is plotted along Y-axis and the time taken by the body is plotted along X-axis.
The area under velocity-time graph gives displacement.
Velocity-time graphs under various conditions are explained as below
(i) Velocity-Time Graph for a Body Moving with Constant Velocity
When a body moves with constant velocity, i.e. its motion is uniform, then its velocity does not change with time.
The graph will be a straight line parallel to the time axis.
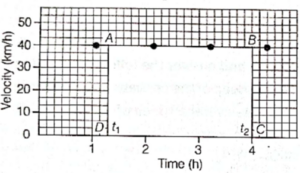
Interpretation
From the graph, it is clear that with the passage of time, there is no change in the velocity, i.e. the body is moving with constant velocity.
Calculation of distance or magnitude of displacement Let us calculate the distance or magnitude of the displacement of a body between time t1 and time t2.
Draw perpendiculars AD and BC from the points corresponding to time t1 and time t2 on the graph.
Now,
AD = BC = velocity of the body
CD = (t2 - t1) = time interval
Thus, AD x CD = area of rectangle ABCD
Also, AD x CD = velocity x time = distance or magnitude of displacement
Thus, magnitude of displacement = area under velocity-time graph
(ii) Velocity-Time Graph for Uniformly Accelerated Motion
In uniformly accelerated motion, the velocity changes by equal amount in equal interval of time. In this case, the velocity-time graph is a straight line passing through the origin.
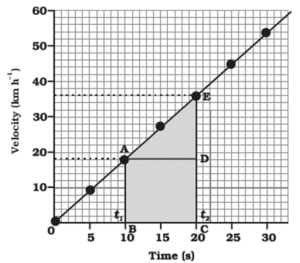
Interpretation
The nature of the graph shows that velocity changes by equal amounts in equal intervals of time. In equal interval of time, i.e. 10 s, the change in velocity is 18 m/s, which remains same, that means the acceleration of the body is constant. Thus, for all uniformly accelerated motion, the velocity-time graph is a straight line.
Calculation of distance or magnitude of displacement :
To determine the distance moved by the car from its velocity-time graph.
The area under the velocity-time graph gives the distance (magnitude of displacement) moved by the car in a given interval of time.
Therefore, S = Area of ABCDE
= Area of the rectangle ABCD + Area of triangle ADE
= AB × BC + \(\frac{1}{2}\)(AD × DE)
(iii) Velocity-Time Graph for Non-uniformly Accelerated Motion
In non-uniformly accelerated motion, velocity-time graphs can have any shape.
If the velocity changes non-uniformly, the velocity-time graph is a curve having increasing or decreasing slope.
Velocity-time graph for non-uniformly accelerated motion is given below

It shows that the velocity of a body (or object) varies non-uniformly with time.
Equations of Motion :
For a body moving along a straight line with uniform acceleration a, the equations of motion relating u (initial velocity), v (velocity after time t), s (displacement in time t), a and t are
- (1) v =u + at (velocity-time relation)
- (2) s =ut + at2 ( displacement-time relation)
- (3) v2 = u2 + 2as (displacement-velocity relation)
Let us obtain these equations by the graphical method.
Consider a body moving along a straight line with uniform acceleration a. Let u=initial velocity of the body (≠ 0),
v = velocity of the body after time t, also called the final velocity and
s = displacement of the body in time t.
Fig. shows the corresponding velocity-time graph. D and B correspond to the initial and final positions of the body.
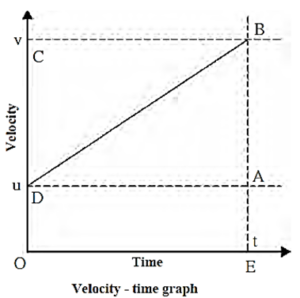
(1) Velocity-time relation
a = \(\frac{Chenge\,in\,velocity}{Time}=\frac{AB}{t}\)
∴ AB = at
BE = BA + AE = BA + DO
∴ v = at + u
∴ v = u + at …(first kinematical equation)
(2) Displacement-time relation
Distance covered in time t= area enclosed within ODBE under velocity-time graph.
s = area of quadrilateral ODBE
= area of rectangle ODAE + area of triangle DAB
= (OE x OD) + \(\frac{1}{2}\)(DA x AB)
Now, OE = DA = t, OD = u and AB = at
s = (t x u) + \(\frac{1}{2}\)(t x at)
∴ s = ut + \(\frac{1}{2}\)at2 …..(second kinematical equation)
(3) Displacement-velocity relation
s = area of trapezium ODBE
= ½ (BE + OE) x OE
Now, OD = u, BE = v and OE = t
∴ s = \(\frac{1}{2}\)(v + u) x t ...(1)
Now a = ∴ t = ...(2)
From Eqs. (1) and (2), we have,
s = \(\frac{1}{2}\)(v + u)
∴ 2as = v2 – u2
v2 = u2 + 2as ….. (third kinematical equation)
Uniform Circular Motion
Uniform circular motion: When a body moves in a circular path with uniform speed, its motion is called uniform circular motion.
In this case, speed, v = \(\frac{circumference}{time}=\frac{2πr}{t}\) where r is the radius of the circular path and t is the time taken by the body to complete one revolution (periodic time).
Direction of velocity in uniform circular motion:
The direction of velocity of a particle performing uniform circular motion is along the tangent to the circle at the position of the particle, in the sense of motion of the particle.
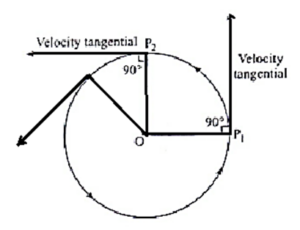
- In uniform circular motion, speed is uniform, velocity is not uniform.
- The magnitude of velocity remains constant, but the direction of velocity changes continuously with time.
- It follows that the motion is accelerated, i.e., the acceleration is not zero.
- The magnitude of acceleration remains constant, but the direction of acceleration changes continuously with time.
- Acceleration is always directed towards the centre of the circle. It is called centripetal acceleration. The corresponding force is called centripetal force.
Examples of uniform circular motion :
- Motion of the earth around the sun
- Motion of the moon around the earth
- Motion of the electron around the nucleus of the hydrogen atom
- Motion of the blades of a fan (when the speed is not changed)
- Motion of a communication satellite (a geostationary satellite used for communication) around the earth.
Click on below link to get PDF from store :
PDF : NCERT-Class-9-Science-Chapter-7-Motion - Notes
PDF : NCERT-Class-9-Science-Chapter-7-Motion - Solution
Main Page : NCERT-Class-9-Science – All chapters notes, solutions, videos, test, pdf.
Previous Chapter : Chapter-6-TISSUES – Online Notes
Next Chapter : Chapter-8- FORCE AND LAWS OF MOTION – Online Notes
