Rotational Dynamics
Class-12th-Physics-Chapter-1-Maharashtra Board
Notes Part-2
|
Characteristics of circular motion
Topics To Be Learn : Part-2 Applications of uniform circular motion
|
Applications of uniform circular motion :
An expression for the maximum safe speed for a vehicle on a horizontal circular road without skidding and its significance :
Consider a car of mass m taking a turn of radius r along a level road. If μs, is the coefficient of static friction between the car tyres and the road surface, the limiting force of friction is fs = μsN = μsmg
where N = mg is the normal reaction, The forces on the car, as seen from an inertial frame of reference are shown in fig.
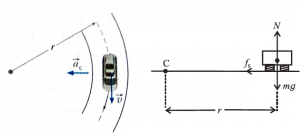
Then, the maximum safe speed vmax with which the car can take the turn without skidding off is set by
maximum centripetal force = limiting force of static friction
mv2max = μsmg or v2max = rμsg
This is the required expression,
Significance : The above expression shows that the maximum safe speed depends critically upon friction which changes with circumstances, e.g., the nature of the surfaces and presence of oil or water on the road. If the friction is not sufficient to provide the necessary centripetal force, the vehicle is likely to skid off the road,
| At a circular bend on a level railway track, the centrifugal tendency of the railway carriages causes the flange of the outer wheels to brush against the outer rail and exert an outward thrust on the rail, Then, the reaction of the outer rail on the wheel flange provides the necessary centripetal force. |
- When a car takes a turn along an level road, apart from the risk of skidding off outward, it also has tendency to roll outward due to an outward torque about the centre of gravity due to the friction force,
- If a bicyclist taking a turn along an unbanked road does not lean inward, an unbalanced outward torque about the centre of gravity due to the friction force will topple the bicyclist outward. The bicyclist must lean inward to counteract this torque (and not to generate a centripetal force).
An expression for the maximum safe speed for a vehicle on a circular horizontal road without toppling/overturning/rollover :
Consider a car of mass m taking a turn of radius r along a level road. As seen from an inertial frame of reference, the forces acting on the car are :
The lateral limiting force of static friction \(\vec{f_s}\) on the wheels acting along the axis of the wheels and towards the centre of the circular path which provides the necessary centripetal force see Fig.
The weight \(vec{m_g}\) acting vertically downwards at the centre of gravity (C.G.)
The normal reaction \(\vec{N}\) of the road on the wheels, acting vertically upwards effectively at the C.G.
Since maximum centripetal force = limiting force of static friction,
mar = \(\frac{mv^2}{r} = f_s\) …..(1)
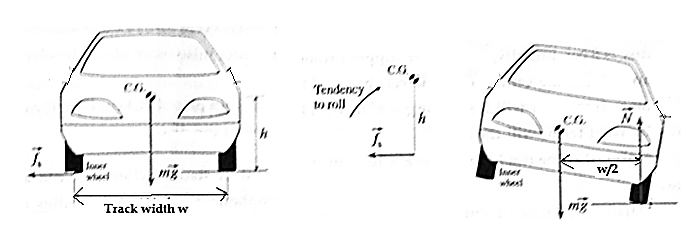
In a simplified rigid-body vehicle model, we consider only two parameters-the height h of the C.G. above the ground and the average distance ‘w’ between the belt and right wheels called the track width.
The friction force \(\vec{f_s}\) on the wheels produces a torque τt that tends to overturn/rollover the car about the outer wheel. Rotation about the front-to-back axis is called roll.
τt = fs.h = \((\frac{mv^2}{r})h\) …….. (2)
When the inner wheel just gets lifted above the ground, the normal reaction \(\vec{N}\) of the road acts on the outer wheels but the weight continues to act at the C.G. Then, the couple formed by the normal reaction and the weight produces a opposite torque τr , which tends to restore the car back on all four wheels ref. Fig.
τr =mg. \((\frac{w}{2})\) …….(3)
The car does not topple as long as the restoring torque τt counterbalances the toppling torque τt
Thus, to avoid the risk of rollover, the maximum speed that the car can have is given by
\((\frac{mv^2}{r})h\) = mg.\((\frac{w}{2})\)
∴\(v_{max}=\sqrt{\frac{rwg}{2h}\) ……(2)
Thus, vehicle tends to roll when the radial acceleration reaches a point where inner wheels of the four-wheeler are lifted off of the ground and the vehicle is rotated outward. A rollover occurs when the gravitational force \(\vec{mg}\) passes through the pivot point of the outer wheels, i.e., the C.G. is above the line of contact of the outer wheels. Equation (3) shows that this maximum speed is high for a car with larger track width and lower centre of gravity.
There will be rollover (before skidding) if τt ≥ τr that is if
fs.h ≥ mg.\((\frac{w}{2})\)
i.e., if
\(\frac{f_s}{mg} ≥ \frac{w}{2}\) or \(\frac{a_r}{g} ≥ \frac{w}{2h}\) or \(\frac{f_s}{μ_s} ≥ \frac{w}{2h}\)
The vehicle parameter ratio \(\frac{w}{2h}\) is called the static stability factor (SSF). Thus, the risk of a rollover is low if SSF ≤ μs. A vehicle will most likely skid out rather than roll if ms is too low, as on wet or icy road.
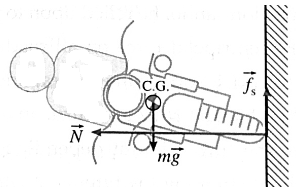
Q. While driving along an unbanked circular road, a two-wheeler rider has to lean with the vertical. Why is it so? With what angle the rider has to lean?
(i) When a bicyclist takes a turn along an unbanked road, the force of friction \(\vec{f_s}\) provides the centripetal force; the normal reaction of the road \(\vec{N}\) is vertically up. If the bicyclist does not lean inward, there will be an unbalanced outward torque about the centre of gravity, fs·h, due to the friction force that will topple the bicyclist outward. The bicyclist must lean inward to counteract this torque (and not to generate a centripetal force) such that the opposite inward torque of the couple formed by and the weight g,
mg·a = fs·h1.
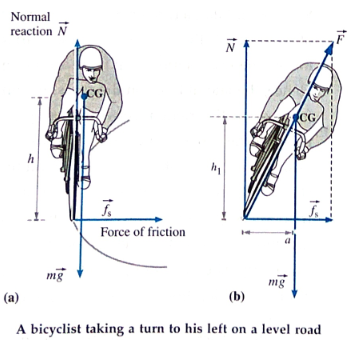
(ii) Since the force of friction provides the centripetal force,
\(f_s=\frac{mv^2}{r}\)
If the cyclist leans from the vertical by an angle q, the angle between \(\vec{N}\) and \(\vec{F}\) as shown in fig (b).
tanθ=\(\frac{f_s}{N}\ = \frac{mv^2/r}{mg}=\frac{v^2}{gr}\)
Hence, the cyclist must lean by an angle
θ =tan-1 \(\frac{v^2}{gr}\)
Q. Show that while riding in “Well of death” the minimum speed necessary to keep the rider from falling is given by \(v=\sqrt{\frac{rg}{μ_s}}\) in usual notations.
The forces exerted on the rider are
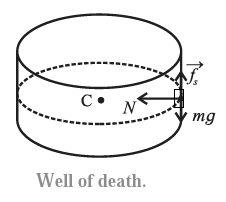
(i) The normal force \(\vec{N}\) exerted by the wall, directed radially inward, is the centripetal force,
(ii) The upward frictional force \(\vec{f_s}\) exerted by the wall, since the motorcycle has a tendency to slide down,
(iii) the downward gravitational force \(\vec{mg}\)
∴ N = mv2/ r and fs = μsN = μs(mv2/ r)
where m is the mass of the rider and v is the speed of the motorcyclist. For the rider not to fall \(\vec{f_s}\) must balance \(\vec{g}\).
μs(mv2/ r) = mg
∴ v2 = rg / μs
∴ \(v=\sqrt{\frac{rg}{μ_s}}\)
which is the required expression.
|
(i) N should always be equal to mv2/r ∴ Nmin = mv2min /r = mg/ms (ii) In this case, fs = μsN is valid only for the minimum speed as fs should always be equal to mg. (iii) During the derivation, the vehicle is assumed to be a particle. In reality, it is not so. During revolutions in such a well, a two-wheeler rider is never horizontal, else, the torque due to her/his weight will topple her/him. (iv) In this case, the angle made by the road surface with the horizontal is 90°, i.e., if the road is banked at 90°, it imposes a lower limit on the turning speed. In the previous sub-section we saw that for an unbanked (banking angle 0) road there is an upper limit for the turning speed. It means that for any other banking angle (0 < θ < 90°), the turning speed will have the upper as well as the lower limit.
|
Banking of a road : To avoid the risk of skidding as well as to reduce the wear and tear of the car tyres, the road surface at a bend is tilted inward, i.e., the outer side of the road is raised above its inner side. This is called banking of road.
- A car while taking a turn performs circular motion.
- If the road is horizontal road, the necessary centripetal force is the force of static friction between the car tyres and the road surface.
- The friction depends upon the nature of the surfaces in contact and the presence of oil and water on the road.
- If the friction is inadequate, a speeding car may skid off the road.
Since the friction changes with circumstances, it cannot be relied upon to provide the necessary centripetal force. Moreover, friction results in fast wear and tear of the tyres.
- On a banked road, the resultant of the normal reaction and the gravitational force can act as the necessary centripetal force.
- Thus, every car can be safely driven on such a banked curve at certain optimum speed, without depending on friction.
Hence, a road should be properly banked at a bend.
Angle of banking : The angle of banking is the angle of inclination of the surface of a banked road at a bend with the horizontal.
Expression for the optimum or most safe speed with which a vehicle can be driven along a curved banked road.
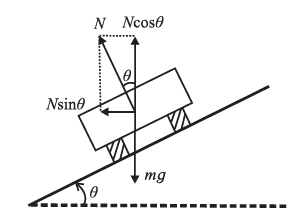
Fig. Optimum (most safe) speed on a banked road
Consider a car taking a left turn along a road of radius r banked at an angle θ for a designed optimum or most safe speed vo. Let m be the mass of the car. In general, the forces acting on the car are
(i) its weight mg acting vertically down
(ii) the normal reaction of the road N perpendicular to the road surface
(iii) the frictional force fs along the inclined surface of the road.
At the optimum speed, frictional force is not relied upon to contribute to the necessary lateral centripetal force.
Thus, ignoring fs , resolve N into two perpendicular components :
N cosθ vertically up and N sinθ horizontally towards the centre of the circular path.
Since there is no acceleration in the vertical direction, N cosθ balances mg and N sinθ provides the necessary centripetal force.
N sinθ = \(\frac{mv_0^2}{r}\) …..(1)
N cosθ = mg …..(2)
∴ \(\frac{N sinθ}{N cosθ}=\frac{\frac{mv_0^2}{r}}{mg}\)
∴ tanθ = \{\frac{v_o^2}{rg}\) or θ =tan-1 \(\frac{v_0^2}{rg}\) …..(3)
Equation (3) gives the expression for the required angle of banking.
From Eq. (3), we can see that
- angle θ depends upon vo, r and g.
- The angle of banking is independent of the mass of a vehicle negotiating the curve.
Also, for a given r and θ, the recommended optimum speed is
vo = \(\sqrt{rgtanθ}\)
| Two factors on which the most safe speed of a car in motion along a banked road depends is
(i) The angle of banking of the road (ii) and the radius of the curved path. |
Expression for (a) the minimum safe speed (b) the maximum safe speed with which a vehicle can negotiate the curve without skidding on a banked circular road which is designed for traffic moving at an optimum or most safe speed vo :
Suppose a car taking a left turn along a road of radius r banked at an angle θ for a designed optimum or most safe speed vo. Let m be the mass of the car. In general, the forces acting on the car are
(i) its weight mg acting vertically down
(ii) the normal reaction of the road N perpendicular to the road surface
(iii) the frictional force fs along the inclined surface of the road.
If μs is the coefficient of static friction between the tyres and road, fs = μsN
(a) For minimum safe speed : If the car is driven at a speed less than the optimum speed vo, it may tend to slide down the inclined surface of the road so that
fs is up the incline, see Fig.
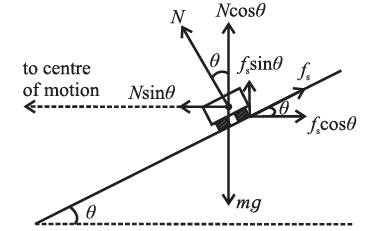
Fig. Minimum safe speed on a banked road
Resolve N and fs into two perpendicular components : N cosθ and fs sinθ vertically up; N sinθ horizontally towards the centre of the circular path while fs cosθ
horizontally outward. So long as the car takes the turn without sliding down, the sum
N cosθ + fs sinθ balances mg, and N sinθ — fs cosθ provides the necessary centripetal force. If vmin is the minimum safe speed without skidding
\(\frac{v^2_{min}}{r}\) = N sinθ — fs cosθ = N(sinθ — μscosθ) ………..(1)
And mg = N cosθ + fs sinθ = N(cosθ + μssinθ) ………..(2)
∴ Dividing Eq. (1) by Eq- (2)
∴ \(\frac{v^2_{min}}{rg}\) = \(\frac{sinθ-μ_s cosθ}{cosθ-μ_s sinθ}\) = \(\frac{tanθ-μ_s}{1+μ_stannθ}\)
∴ \(v_{min}=\sqrt{\frac{rg(tanθ-μ_s)}{1+μ_stannθ}}\)………..(3)
For tanθ ≤ μs (as on most rough roads),
vmin = 0 (i.e., a car can be brought to a halt without sliding down).
(b) For maximum safe speed :If the car is driven fast enough, at a speed greater than the optimum speed v, it may skid off up the incline so that fs is down the incline, see Fig.
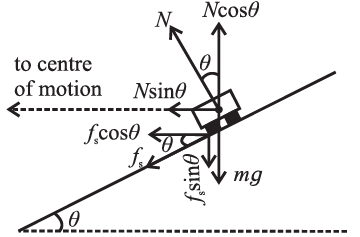
Fig. Maximum safe speed on a banked road
Resolve N and fs into two perpendicular components : N cosθ vertically up and fs sinθ vertically clown; N sinθ and fs cosθ horizontally towards the centre of the circular path. So long as the car takes the turn without skidding off, the horizontal components N sinθ and fs cosθ together provide the necessary centripetal force, and N cosθ balances the sum mg + fs sinθ. If vmax, is the maximum safe speed without skidding,
\(\frac{v^2_{max}}{r}\)= N sinθ + fs cosθ = N(sinθ + μscosθ) ………..(4)
And N cosθ =mg + fs sinθ = mg + μsNsinθ
∴ mg = N(cosθ - μssinθ) ………..(5)
Dividing Eq. (4) by Eq (5)
∴ \(\frac{v^2_{max}}{rg}\) = \(\frac{sinθ+μ_s cosθ}{cosθ-μ_s sinθ}\) = \(\frac{tanθ+μ_s}{1-μ_stannθ}\)
∴ \(v_{max}=\sqrt{\frac{rg(tanθ+μ_s)}{1-μ_stannθ}}\) ………..(6)
1- μstanθ = 0, i.e. μs = cotθ, vmax = ∞
Ignoring few special cases, the maximum value of μs = 1.
Thus, for θ ≥ 45°, vmax = ∞
i.e., on a heavily banked road a car is unlikely to skid up the incline and the minimum limit is more important.
Kinetic friction between road and tyres : When a car takes a turn on a level road, the point of contact of the wheel with the surface is instantaneously stationary if there is no slipping. Hence, the lateral force on the car is the limiting force of static friction between the tyres and road. Lateral forces allow the car to turn. As long as the wheels are rolling, there is lateral force of static friction and longitudinal force of rolling friction. Longitudinal forces, which act in the direction of motion of the car body (or in the exact opposite direction), control the acceleration or deceleration of the car and therefore the speed of the car. These are the wheel force, rolling friction, braking force and air drag. if the car skids, the friction force is kinetic friction; more importantly, the direction of the friction force then changes abruptly from lateral to that opposite the velocity of skidding and not towards the centre of the curve, so that the car cannot continue in its curved path. |
Pendulum : A tiny mass (assumed to be a point object and called a bob) connected to a long, flexible, massless, inextensible string, and suspended to a rigid support is called a pendulum. If the string is made to oscillate in a single vertical plane, we call it a simple pendulum
Conical pendulum : A conical pendulum is a simple pendulum whose bob revolves in a horizontal circle with constant speed such that the string describes the surface of an imaginary right circular cone. OR
Expression for the angular speed of the bob of a conical pendulum :
A conical pendulum is a small bob suspended from a string and set in UCM in a horizontal plane with the centre of its circular path below the point of suspension such that the string makes a constant angle θ with the vertical.
Consider a conical pendulum of string length L with its bob of mass m performing UCM along a circular path of radius r (Fig).
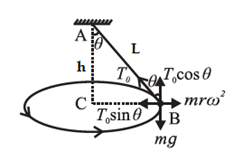
At every instant of its motion, the bob is acted upon by its weight mg and the tension T in the string.
If the constant angular speed of the bob is w, the necessary horizontal centripetal force is
T0 = mω2r
T0. is the resultant of the tension in the string and the weight. Resolve T into components T0 cosθ vertically opposite to the weight of the bob and
T0 sinθ horizontal. T0 cosθ balances the weight. T0 sinθ is the necessary centripetal force.
∴ T0 sinθ = mω2r ……… (1)
and T0 cosθ = mg ……… (2)
Dividing Eq. (1) by Eq. (2)
Tanθ = \(\frac{ω^2}{r}\)
From the diagram,
Tanθ = \(\frac{r}{AC}\) = \(\frac{r}{h}\) = \(\frac{r}{Lcosθ}\) ……… (3)
∴ \(\frac{r}{h}\) = \(\frac{ω^2r}{g}\)
∴ ω2 = \(\frac{g}{h}\) = \(\frac{g}{Lcosθ}\) ……… (4)
The angular speed of the bob,
ω = \(\sqrt{\frac{g}{h}}\) = \(\sqrt{\frac{g}{Lcosθ}}\) ……… (5)
From Eq. (4), cosθ=g/ω2L. Therefore, as ω increases, cosθ decreases and θ increases
Expression for the frequency of revolution of the bob of a conical pendulum :
If n is the frequency of revolution of the bob,
ω = 2πn = \(\sqrt{\frac{g}{Lcosθ}}\)
∴ n = \(\frac{1}{2π}\sqrt{\frac{g}{Lcosθ}}\) ..is the required expression for the frequency.
From the above expression, we can see that
(i) n ∝ \(\sqrt{g}\) (g is the acceleration due to gravity at the place.)
(ii) n ∝ \(\frac{1}{\sqrt{L}}\)
(iii) n ∝ \(\frac{1}{\sqrt{cosθ}}\) …..(if θ increases, cosθ decreases and n increases)
(iv) The frequency is independent of the mass of the bob.
Period of a conical pendulum and an expression for it : The period of a conical pendulum is the time taken by its bob to complete one revolution in a horizontal circle with constant speed.
For the derivation, refer above expression up to Eq. (5) and continue.
If TP is the period, ω = 2π/TP
∴ TP = 2π/ω = \(2π\sqrt{\frac{Lcosθ}{g}}\) is the required expression.
Note - L cosθ =AC = h, where h is the axial height of the cone.
∴ TP = \(2π\sqrt{\frac{h}{g}}\)
This shows that the period of a conical pendulum is the same as that of a simple pendulum of length h
From the above expression, we can see that
(i) Time period TP ∝ \(\sqrt{L}\)
(ii) TP ∝ \(\frac{1}{\sqrt{g}}\)
(iii) TP ∝ \(\sqrt{cosθ}\) …..(if θ increases, cosθ and TP decreases)
(iv) The period is independent of the mass of the bob.
| <<-Previous Part | Next part->> |
Click on below link to get PDF from store:
PDF : MSBSHSE-Class-12-Physics-Chapter-1-Rotational Dynamics-Book
PDF : MSBSHSE-Class-12-Physics-Chapter-1-Rotational Dynamics-Notes
PDF : MSBSHSE-Class-12-Physics-Chapter-1-Rotational Dynamics-Solution
Class -12 -Physics -All 16 Chapters Notes (16-PDF)-Rs.135
Class -12 -Physics -All 16 Chapters Solutions (16-PDF)-Rs.131
All Notes and Solutions-Class-12-Physics-16 Chapters-(32 PDF) Rs.244
Useful links :
| Main Page : - Maharashtra Board Class 12-Physics - All chapters notes, solutions, videos, test, pdf.
Books : MSBSHSE -Class 12th Science Text Books – Chapter wise PDF for download Next Chapter :Chapter-2-Mechanical Properties of Fluids - Online Notes |